Das wusste schon de Morgan
Aufgabenstellung
Die boolesche Operation kann unter Verwendung der booleschen Operation aus der booleschen Operation erzeugt werden. Und auch umgekehrt, kann aus unter Verwendung von erzeugt werden.
Bauen Sie und . Entwickeln Sie zunächst die benötigen Formeln und entwerfen Sie dann die dazu entsprechenden Schaltungen.
Grundlagen
| A | B | A B | A B |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
De Morganschen Gesetze
NOT (A AND B) ist dasselbe wie (NOT A) OR (NOT B)
| A | B | ||
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
NOT (A OR B) ist dasselbe wie (NOT A) AND (NOT B):
| A | B | ||
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
Schaltplan zu De Morgan
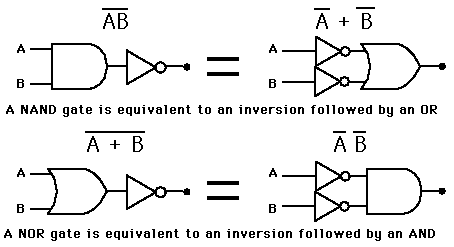
Aus den De Morganschen Gesetzen können wir nun AND und OR herleiten
AND
- Aus dem ersten De Morganschen Gesetz gilt
- Dies negieren wir nun nochmal um durch die Doppelte Negierung, die Negierung aufzuheben
OR
- Aus dem zweiten De Morganschen Gesetz gilt
- Dies negieren wir nun nochmal um durch die Doppelte Negierung, die Negierung aufzuheben
Zaun oder Gatter – das ist hier die Frage
Untersuchen Sie anhand von Wahrheitstafeln, ob
!a !b c + !a b !c + a !b !c + a b c
und
Xor( Xor(a,b), c)
identisch sind.
Lösung
Um die beiden Ausdrücke und anhand von Wahrheitstafeln zu vergleichen, erstellen wir zunächst die Wahrheitstafeln für beide Ausdrücke und prüfen dann, ob die Ergebnisse in allen Fällen übereinstimmen.
Wahrheitstafel für
| a | b | c | !a | !b | !a!bc | !ab!c | a!b!c | abc | !a!bc + !ab!c + a!b!c + abc |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
Wahrheitstafel für
- Berechnen wir zunächst :
| a | b | a ⊕ b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- Berechnen wir dann :
| a | b | c | a ⊕ b | (a ⊕ b) ⊕ c |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
Vergleich der Wahrheitstafeln
| a | b | c | !a!bc + !ab!c + a!b!c + abc | (a ⊕ b) ⊕ c |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Wir sehen, dass die Ergebnisse in allen Fällen übereinstimmen. Daher sind die beiden Ausdrücke und identisch.