Blatt-11-Fehlererkennung

Fehlererkennung und Kompression

Cyclic Redundancy Check

Aufgabenstellung

Ermitteln Sie zum Datenblock 1011 die Prüfsumme mit Hilfe des 110101. Führen Sie anschließend auch die Überprüfung durch.

Wichtiges Know-How für CRC

• Methode zur Fehlererkennung
• Gut geeignet, um zufällige Fehler zu erkennen
• Kann keine Fehler verhindern oder exakt lokalisieren
• Überprüft nur, ob Fehler aufgetreten sind
• Effizient in Berechnung und Überprüfung
• Erkennt Einzelbit- und Burst-Fehler
• Nicht geeignet, um beabsichtigte Manipulationen zu erkennen
• Sicherstellung der Datenintegrität in:
  • Netzwerkkommunikation (z.B. Ethernet, Wi-Fi)
  • Speichergeräten (z.B. Festplatten, SSDs)
  • Dateisystemen (z.B. ZFS, Btrfs)
  • Datenübertragung (z.B. USB, serielle Kommunikation)
  • Telekommunikation (z.B. Modems, Mobilfunk)
  • Softwareanwendungen (z.B. Dateiarchivierung, Datensicherung)
  • Industrieanwendungen (z.B. Modbus, CAN-Bus)
• Implementierung in Hardware und Software
• Jeder Block bekommt eine Prüfsumme angehängt
• Verfahren beruht auf Polynomdivision
• Empfänger rechnet Datenpaket modulo CRC-Polynom
• Verschiedene Varianten (CRC-8, CRC-16, CRC-32)
• Grenzen: Fehler nicht lokalisieren oder korrigieren, mögliche Kollisionen bei großen Datenmengen

Was ist ein Generatorpolynom?

• Dient zur Erzeugung von Prüfbits in unserem Fall die Bitfolge (110101)
• Ein Generatorpolynom ist immer ein Polynom von Grad $n$
• Beispielsweise:

$$G(x)=x^3+x+1$$

• Ist als Bitfolge dargestellt: $1011$, da wir $1x^3$ , $1x^1$ und $1x^0$ haben
• Die Null kommt daher, da $x^2$ nicht enthalten ist ($0x^2$)

Lösung

• Gegeben
  • Datenblock : 1011
  • Generatorpolynom : 110101
  • Generatorpolynom könnte auch als Polynom vorliegen: (falls Prof es mal so macht)

$$G(x)=x^5+x^4+x^2+1$$

• was äquivalent zu dem hier ist (fürs Verständnis)

$$G(x)=1x^5+1x^4+0x^3+1x^2+0x^1+1x^0$$

Schritt 1 - Vorbereiten des Datenblocks

• Datenblock wird um den Grad von $G$ erweitert
  • wird gemacht um die Division später durchführen zu können
  • ohne diese kommt man nicht auf die Korrekte Prüfsumme
• $\text{Grad(G)}=5$, da $x^5$ unser größtes $x$ ist

$$1011\to 101100000$$

Schritt 2 - Berechnung der Prüfsumme

• Nun dividieren wir mit dem $XOR(\oplus )$ - Operator und den Bits welche $G$ repräsentieren
• Zur Erinnerung:

A	B	A ⊕ B
0	0	0
0	1	1
1	0	1
1	1	0

• Berechnung:

101100000 : 110101 = 
110101
------
011001

• Nach der ersten Berechnung erhalten wir $011001$
• Nun führen wir die Division erneut durch, wobei wir die voranstehende 0 ignorieren

101100000 : 110101 = 
110101
------
011001
 110101

• Da unser Generatorpolynom länger ist als unser Zwischenergebnis, ziehen wir die restlichen Nuller nun mit runter

101100000 : 110101 = 
110101↓↓↓
------↓↓↓
011001000
 110101↓↓
 ------↓↓
 00011100 → Rest 

• Wir haben nun alle Bits in unseren Datenpaket benutzt und bekommen als Rest $00011100$
• Dieser Rest ist nun gleichzeitig unsere Prüfsumme

Schritt 3 - Bildung des CRC-Wertes

• Nun hängen wir diese Prüfsumme an unser Datenpaket an
• Ursprüngliche Datenblock: $1011$
• Hinzufügen von Prüfsumme (wobei voranstehende 0er ignoriert werden)

$$1011+11100=101111100$$

Schritt 4 - Überprüfung durchführen

• Daten wurden fehlerfrei übertragen, wenn bei der Divison als Rest 0 rauskommt
• Wir benutzen hier den CRC-Wert welchen wir zuvor berechnet haben und teilen diesen durch unseren Generatorpolynom

101111100 : 110101 
110101
------
0110101
 110101
 ------
 000000 → Rest ist 0

• Da der Rest 0 ist, hat kein Übertragungsfehler stattfgefunden

Hamming-Distanz

Aufgabenstellung

Gegeben sind die Datenblöcke 10011101101, 11111101101, 01111101101 und 10011101101. Wie groß ist die Hamming-Distanz?

Wichtige Informationen zum Hamming-Abstand

• “Maß für die Unterschiedlichkeit von Zeichenketten”
• Misst die Anzahl der Positionen, an denen zwei gleich lange Bitfolgen unterschiedlich sind
• Wesentlich für die Theorie der Kodierung und Fehlerkorrektur
• Gut geeignet, um die Ähnlichkeit oder Differenz zwischen zwei Datenfolgen zu bestimmen
• üblich sind Hamming-Distanzen von 4 bis

Unter dem Hamming-Abstand eines Codes versteht man das Minimum aller Abstände zwischen verschiedenen Wörtern innerhalb des Codes.

• Anwendung in:
  • Datenkompression
  • Fehlererkennung und -korrektur
  • DNA-Sequenzanalyse
  • Bild- und Signalverarbeitung
  • Informationstheorie
• Berechnung:
  • Vergleich der Bits an jeder Position der beiden Bitfolgen
  • Zählen der unterschiedlichen Bits
• Grenzen: Nur geeignet für Bitfolgen gleicher Länge
• Bedeutung in der Praxis:
  • Bestimmung der Mindestanzahl an Änderungen, die erforderlich sind, um eine Bitfolge in eine andere zu verwandeln
  • Grundlage für viele Algorithmen in der Datenverarbeitung und -analyse

Unter dem Hamming-Abstand eines Codes versteht man das Minimum aller Abstände zwischen verschiedenen Wörtern innerhalb des Codes.

Lösung

$$\begin{array}{rl}\text{1. Datenblock}& :10011101101\\ \text{2. Datenblock}& :11111101101\\ \text{3. Datenblock}& :01111101101\\ \text{4. Datenblock}& :10011101101\end{array}$$

• Vergleiche die Hamming-Abstände
• Vergleich 1 & 2:

Vergleich 1

Vergleich 1 & 2:
10011101101
11111101101
-----------
01100000000 → Hamming Abstand ist 2

Vergleich 1 & 3:
10011101101
01111101101
-----------
11100000000 → Hamming Abstand ist 3

Vergleich 1 & 4:
10011101101
10011101101
-----------
00000000000 → Hamming Abstand ist 0

Vergleich 2

Vergleich 2 & 3:
11111101101
01111101101
-----------
10000000000 → Hamming Abstand ist 1

Vergleich 2 & 4:
11111101101
10011101101
-----------
01100000000 → Hamming Abstand ist 2

Vergleich 3

Vergleich 3 & 4:
01111101101
10011101101
-----------
11100000000 → Hamming Abstand ist 3

• Kleinster Hamming Abstand ist 0 (1 & 4 sind identisch)
  • $h=0$

Kompression

Aufgabenstellung

Komprimieren Sie die Zeichenfolge ABABCDAB einmal mit Hilfe des LZ77-Algorithmus und anschließend mit der Huffman-Kodierung.

LZ77

Need to Know: LZ77 (Lempel-Ziv 1977)

• Definition: LZ77 ist ein verlustfreies Datenkompressionsverfahren, entwickelt von Abraham Lempel und Jacob Ziv im Jahr 1977.

• Funktionsweise:

  • Sliding Window: Durchsucht die Eingabedaten nach wiederholten Mustern.
  • Verweise: Ersetzt Wiederholungen durch Verweise auf frühere Vorkommen (Abstand und Länge).
  • Literals: Zeichen ohne Übereinstimmungen werden direkt gespeichert.

• Vorteile:

  • Effizient bei wiederholten Datenmustern.
  • Einfach zu implementieren und zu verstehen.
  • Flexibel für Text- und Binärdaten.

• Anwendungen:

  • Dateikomprimierung: Grundlage für Formate wie ZIP, gzip und PNG.
  • Netzwerkprotokolle: Reduziert Datenübertragungsgrößen in Protokollen wie HTTP.
  • Datenbanken: Verringert Speicherbedarf durch Komprimierung.

$$ \text{Wort}=ABABCDAB $$

 
ABABCDAB
 
 
| Lexikon         | Vorschaufenster | REST VOM WORT |
| 0 1 2 3 4 5 6 7 |                 |               |
----------------------------------------------------|
|                 | ABAB            | CDAB          | → (0,0,A)
|               A | BABC            | DAB           | → (0,0,B)
|             A B | ABCD            | AB            | → (6,2,C)
|       A B A B C | DAB             |               | → (6,2,D)
|     A B A B C D | AB              |               | → (2,2,-)
| A B A B C D A B |                 |               | → (-,-,-)

→ Das Ergebis lautet :

$$[(0,0,A),(0,0,B),(6,2,C),(6,2,D),(2,2,-)]$$

Huffmann

$$ \text{Wort}=ABABCDAB $$

Schritt 1 - Buchstaben zählen

• Zählen wie oft jeder Buchstabe drankommt

$A$	$B$	$C$	$D$
3	3	1	1

Schritt 2 - zwei seltensten Buchstaben verknoten

• $C$ und $D$ kommen jeweils nur einmal vor, weswegen sie verknüpft werden
• Knoten $CD$ entsteht mit Häufigkeit 1+1=2

Schritt 3 - Diesen Knoten mit anderem seltensten verknoten

• $A$ und $B$ sind beide gleich Häufig wir können eins auswählen.
• Gewählt sei $B$
• Es entsteht der Knoten $BCD$ mit Häufigkeit 2+3 = 5

Schritt 4 - Schritt 3 wiederholen bis fertig

• $A$ ist unser einziger Knoten
• Wir verknoten diesen mit $BCD$
• $ABCD$ ist die Wurzel mit Häufigkeit 8

Schritt 5 - Pfade und Blätter beschriften

• Jeder linke Pfad bekommt eine 0
• Jeder rechte Pfad eine 1
• Beschrifte danach dementsprechend die Blätter

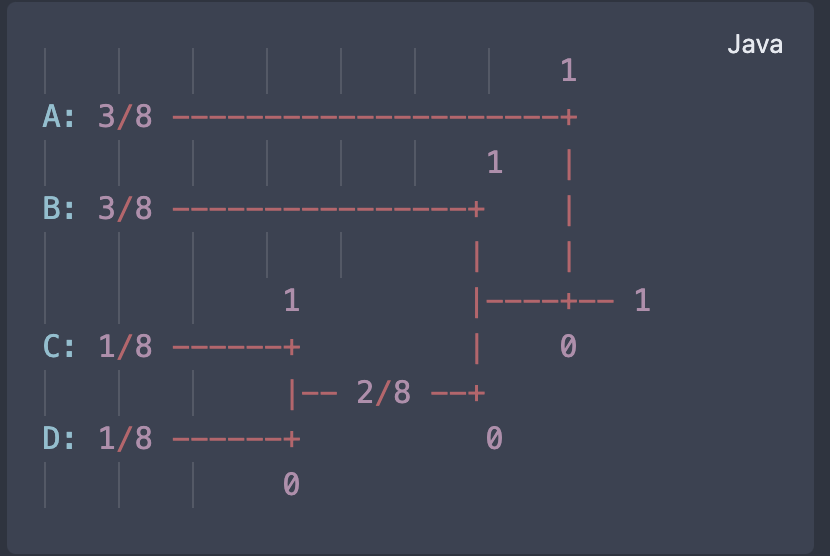
							1
A: 3/8 ---------------------+
						1	|
B: 3/8 ----------------+    |
					   |    |
			 1    	   |----+-- 1
C: 1/8 ------+         |    0
			 |-- 2/8 --+
D: 1/8 ------+          0
			 0

• $A\to 1$
• $B\to 01$
• $C\to 001$
• $D\to 000$

Schritt 6 - Ersetze Buchstaben

$$\text{Wort}=ABABCDAB$$

• $A\to 1$
• $B\to 01$
• $C\to 001$
• $D\to 000$

$$101101001000101$$

Nice to Know

• Das Wort lautet 01000001 01000010 01000001 01000010 01000011 01000100 01000001 01000010 in Binärdarstellung (56 Bits)
• Wir konnten es nun auf 101101001000101 (15 Bit) komprimieren
• Wir ersparen uns damit $\approx 73.21\%$